Get Started

Lucas da Cunha Godoy

library(drmr)
library(sf) ## "mapping"

Linking to GEOS 3.12.1, GDAL 3.8.4, PROJ 9.4.0; sf_use_s2() is TRUE

library(ggplot2) ## graphs
library(bayesplot) ## and more graphs

This is bayesplot version 1.13.0

- Online documentation and vignettes at mc-stan.org/bayesplot

- bayesplot theme set to bayesplot::theme_default()

   * Does _not_ affect other ggplot2 plots

   * See ?bayesplot_theme_set for details on theme setting

library(dplyr)

Attaching package: 'dplyr'

The following object is masked from 'package:drmr':

    between

The following objects are masked from 'package:stats':

    filter, lag

The following objects are masked from 'package:base':

    intersect, setdiff, setequal, union

We will use a dataset included with the package. In particular, this data is similar to the one analyzed in Fredston et al. (2025). To load the data, we run:

data(sum_fl)

Data processing & splitting

To assess model predictions, the chunk below splits the data into train and test.

## 5 years-ahead predictions
first_year_forecast <- max(sum_fl$year) - 5

first_id_forecast <-
  first_year_forecast - min(sum_fl$year) + 1

years_all <- length(unique(sum_fl$year))
years_train <- years_all[years_all < first_id_forecast]
years_test <- years_all[years_all >= first_id_forecast]

## splitting data
dat_test <- sum_fl |>
  filter(year >= first_year_forecast)

dat_train <- sum_fl |>
  filter(year < first_year_forecast)

Finally, I transform our response variable into a density.

dat_train <- dat_train |>
  mutate(dens = y / area_km2,
         .before = y)

dat_test <- dat_test |>
  mutate(dens = y / area_km2,
         .before = y)

The elements we need to fit a DRM are:

• A response variable representing a density

• A variable encoding time-points

• A variable encoding patches (or sites).

The current version of the functions assumes that we have rows in the dataset for every combinations of “time” and “site”. That is, if a dataset comprises observations around the density of a given species across 20 years and 10 patches, we expect to have 20 rows in the dataset per patch. Equivalently, we would expect 10 rows in the dataset per year.

The first and last 10 rows of the dat_train object look as follows:

head(dat_train[, c("year", "patch",  "y", "stemp")],
     n = 10)

# A tibble: 10 × 4
    year patch     y stemp
   <dbl> <int> <dbl> <dbl>
 1  1982     1     2  24.5
 2  1983     1     9  25.4
 3  1984     1     0  20.5
 4  1985     1     0  24.5
 5  1986     1     0  22.6
 6  1987     1     0  25.9
 7  1988     1     1  23.2
 8  1989     1     0  25.8
 9  1990     1     2  24.5
10  1991     1     4  25.4

tail(dat_train[, c("year", "patch",  "y", "stemp")],
     n = 10)

# A tibble: 10 × 4
    year patch     y stemp
   <dbl> <int> <dbl> <dbl>
 1  2001    10     0  11.1
 2  2002    10     0  11.6
 3  2003    10     0  10.4
 4  2004    10     0  10.0
 5  2005    10     0  11.1
 6  2006    10     0  11.8
 7  2007    10     0  10.3
 8  2008    10     0  10.2
 9  2009    10     0  10.3
10  2010    10     0  10.2

Note that, stemp is an explanatory variable denoting the sea surface temperature (SST).

Fitting & diagnosing a model

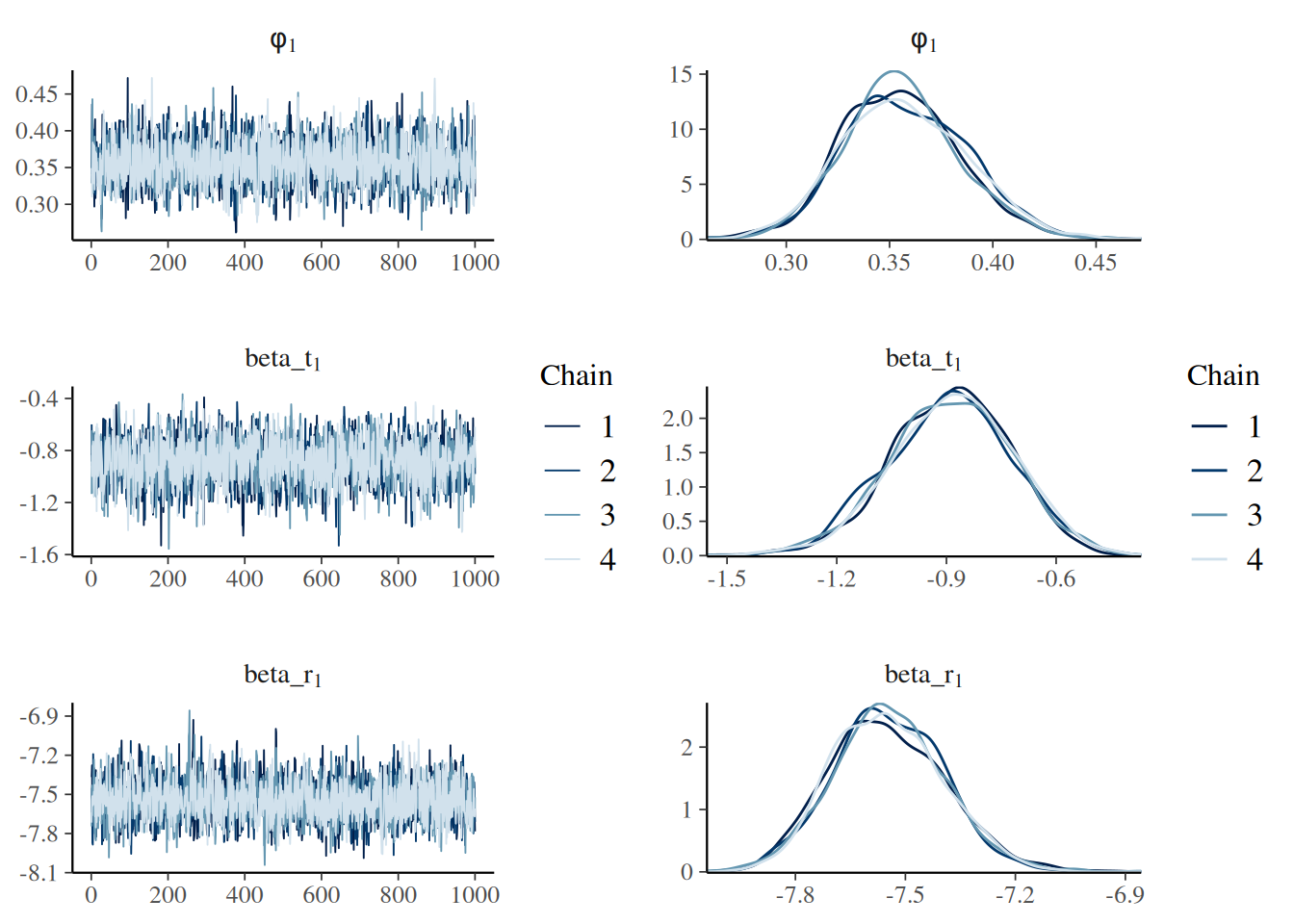
Provided the dataset is properly formatted, a simple model considering the existance of 8 age groups and a natural mortality rate of 0.25 can be fit as follows:

mcmc_samples <-
  fit_drm(.data = dat_train,
          y_col = "dens",
          time_col = "year",
          site_col = "patch",
          n_ages = 8,
          m = 0.25,
          seed = 2025)

Running MCMC with 4 parallel chains...

Chain 1 Iteration:    1 / 2000 [  0%]  (Warmup) 

Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 1 Exception: gamma_lpdf: Random variable is 0, but must be positive finite! (in '/tmp/RtmpBXDoDm/model-247b6426e971.stan', line 595, column 4 to column 54)

Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 1 

Chain 2 Iteration:    1 / 2000 [  0%]  (Warmup) 

Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 2 Exception: gamma_lpdf: Random variable is 0, but must be positive finite! (in '/tmp/RtmpBXDoDm/model-247b6426e971.stan', line 595, column 4 to column 54)

Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 2 

Chain 3 Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 3 Iteration:  100 / 2000 [  5%]  (Warmup) 

Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 3 Exception: gamma_lpdf: Random variable is 0, but must be positive finite! (in '/tmp/RtmpBXDoDm/model-247b6426e971.stan', line 595, column 4 to column 54)

Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 3 

Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 3 Exception: gamma_lpdf: Random variable is 0, but must be positive finite! (in '/tmp/RtmpBXDoDm/model-247b6426e971.stan', line 595, column 4 to column 54)

Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 3 

Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 3 Exception: gamma_lpdf: Random variable is 0, but must be positive finite! (in '/tmp/RtmpBXDoDm/model-247b6426e971.stan', line 595, column 4 to column 54)

Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 3 

Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 3 Exception: gamma_lpdf: Random variable is 0, but must be positive finite! (in '/tmp/RtmpBXDoDm/model-247b6426e971.stan', line 595, column 4 to column 54)

Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 3 

Chain 4 Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 4 Iteration:  100 / 2000 [  5%]  (Warmup) 

Chain 4 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 4 Exception: gamma_lpdf: Random variable is 0, but must be positive finite! (in '/tmp/RtmpBXDoDm/model-247b6426e971.stan', line 595, column 4 to column 54)

Chain 4 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 4 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 4 

Chain 4 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 4 Exception: gamma_lpdf: Random variable is 0, but must be positive finite! (in '/tmp/RtmpBXDoDm/model-247b6426e971.stan', line 595, column 4 to column 54)

Chain 4 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 4 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 4 

Chain 4 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 4 Exception: gamma_lpdf: Random variable is 0, but must be positive finite! (in '/tmp/RtmpBXDoDm/model-247b6426e971.stan', line 595, column 4 to column 54)

Chain 4 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 4 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 4 

Chain 4 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 4 Exception: gamma_lpdf: Random variable is 0, but must be positive finite! (in '/tmp/RtmpBXDoDm/model-247b6426e971.stan', line 595, column 4 to column 54)

Chain 4 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 4 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 4 

Chain 1 Iteration:  100 / 2000 [  5%]  (Warmup)
Chain 1 Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 2 Iteration:  100 / 2000 [  5%]  (Warmup)
Chain 3 Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 4 Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 1 Iteration:  300 / 2000 [ 15%]  (Warmup)
Chain 2 Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 3 Iteration:  300 / 2000 [ 15%]  (Warmup)
Chain 4 Iteration:  300 / 2000 [ 15%]  (Warmup)
Chain 1 Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 2 Iteration:  300 / 2000 [ 15%]  (Warmup)
Chain 3 Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 4 Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 1 Iteration:  500 / 2000 [ 25%]  (Warmup)
Chain 2 Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 3 Iteration:  500 / 2000 [ 25%]  (Warmup)
Chain 1 Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 4 Iteration:  500 / 2000 [ 25%]  (Warmup)
Chain 2 Iteration:  500 / 2000 [ 25%]  (Warmup)
Chain 3 Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 4 Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 1 Iteration:  700 / 2000 [ 35%]  (Warmup)
Chain 2 Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 3 Iteration:  700 / 2000 [ 35%]  (Warmup)
Chain 4 Iteration:  700 / 2000 [ 35%]  (Warmup)
Chain 1 Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 2 Iteration:  700 / 2000 [ 35%]  (Warmup)
Chain 3 Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 4 Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 1 Iteration:  900 / 2000 [ 45%]  (Warmup)
Chain 4 Iteration:  900 / 2000 [ 45%]  (Warmup)
Chain 2 Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 3 Iteration:  900 / 2000 [ 45%]  (Warmup)
Chain 1 Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 1 Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 4 Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 4 Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 2 Iteration:  900 / 2000 [ 45%]  (Warmup)
Chain 3 Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 3 Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 4 Iteration: 1100 / 2000 [ 55%]  (Sampling)
Chain 1 Iteration: 1100 / 2000 [ 55%]  (Sampling)
Chain 2 Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 2 Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 3 Iteration: 1100 / 2000 [ 55%]  (Sampling)
Chain 2 Iteration: 1100 / 2000 [ 55%]  (Sampling)
Chain 4 Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 1 Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 3 Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 4 Iteration: 1300 / 2000 [ 65%]  (Sampling)
Chain 1 Iteration: 1300 / 2000 [ 65%]  (Sampling)
Chain 2 Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 3 Iteration: 1300 / 2000 [ 65%]  (Sampling)
Chain 4 Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 2 Iteration: 1300 / 2000 [ 65%]  (Sampling)
Chain 1 Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 3 Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 4 Iteration: 1500 / 2000 [ 75%]  (Sampling)
Chain 1 Iteration: 1500 / 2000 [ 75%]  (Sampling)
Chain 2 Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 3 Iteration: 1500 / 2000 [ 75%]  (Sampling)
Chain 4 Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 2 Iteration: 1500 / 2000 [ 75%]  (Sampling)
Chain 1 Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 3 Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 4 Iteration: 1700 / 2000 [ 85%]  (Sampling)
Chain 1 Iteration: 1700 / 2000 [ 85%]  (Sampling)
Chain 2 Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 4 Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 3 Iteration: 1700 / 2000 [ 85%]  (Sampling)
Chain 2 Iteration: 1700 / 2000 [ 85%]  (Sampling)
Chain 1 Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 3 Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 4 Iteration: 1900 / 2000 [ 95%]  (Sampling)
Chain 1 Iteration: 1900 / 2000 [ 95%]  (Sampling)
Chain 2 Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 4 Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 4 finished in 4.2 seconds.
Chain 3 Iteration: 1900 / 2000 [ 95%]  (Sampling)
Chain 1 Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 2 Iteration: 1900 / 2000 [ 95%]  (Sampling)
Chain 1 finished in 4.4 seconds.
Chain 2 Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 3 Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 2 finished in 4.6 seconds.
Chain 3 finished in 4.5 seconds.

All 4 chains finished successfully.
Mean chain execution time: 4.4 seconds.
Total execution time: 4.8 seconds.

The mcmc_samples object is a named list. One of its positions is called stanfit. We can use the stanfit position as if it was the output of a cmdstanr model. For instance, to assess the convergence of the MCMC, one can run:

mcmc_samples$stanfit$draws(variables = c("phi",
                                         "beta_t",
                                         "beta_r")) |>
  mcmc_combo(combo = c("trace", "dens_overlay"),
             facet_args = list(labeller = label_parsed))

Fredston, Alexa, Daniel Ovando, Lucas da Cunha Godoy, Jude Kong, Brandon Muffley, James T Thorson, and Malin Pinsky. 2025. “Dynamic Range Models Improve the Near-Term Forecast for a Marine Species on the Move.” Ecology Letters 00: (under review). https://doi.org/10.32942/X24D00.